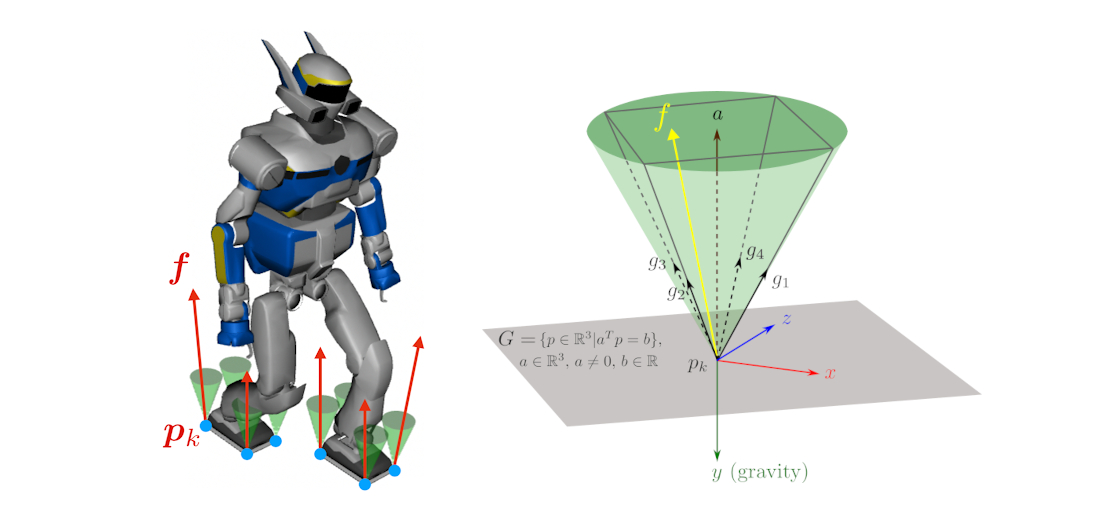
The point contact model and 3D friction cones
Maintaining balance is one of the crucial things for roboticists working with mobile robots, especially with humanoid robots. An example of a walking HRP-2 robot is shown in the teaser figure.
When a foot sole of HRP-2 is in contact with a surface, for example, the ground plane, the contact must remain fixed because otherwise the robot is at risk of falling. Therefore, it is of key interest to derive what we call the contact stability condition for such type of fixed contact.
In this article, we consider the contact point $p_k$ located at the right foot sole of HRP-2 in the teaser example. We discuss the contact stability condition of this point contact model followed by its linear approximation.